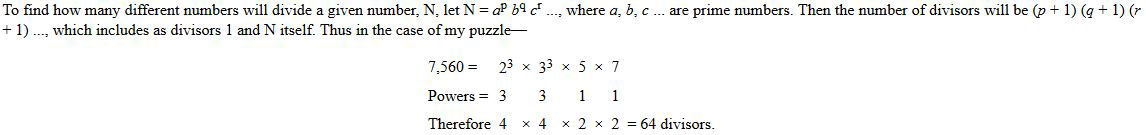This puzzle amounts to finding the smallest possible number that has exactly sixty-four divisors, counting 1 and the number itself as divisors. The least number is 7,560. The pilgrims might, therefore, have ridden in single file, two and two, three and three, four and four, and so on, in exactly sixty-four different ways, the last manner being in a single row of 7,560.

The Merchant was careful to say that they were going over a common, and not to mention its size, for it certainly would not be possible along an ordinary road!

To find the smallest number that has a given number of divisors we must proceed by trial. But it is important sometimes to note whether or not the condition is that there shall be a given number of divisors and no more. For example, the smallest number that has seven divisors and no more is 64, while 24 has eight divisors, and might equally fulfil the conditions. The stipulation as to "no more" was not necessary in the case of my puzzle, for no smaller number has more than sixty-four divisors.

*Si ignoras el significado de alguna palabra, utiliza el diccionario online.