The 8 cheeses can be removed in 33 moves, 10 cheeses in 49 moves, and 21 cheeses in 321 moves. I will give my general method of solution in the cases of 3, 4, and 5 stools.

Write out the following table to any required length:

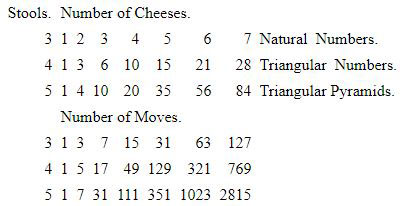
The first row contains the natural numbers. The second row is found by adding the natural numbers together from the beginning. The numbers in the third row are obtained by adding together the numbers in the second row from the beginning. The fourth row contains the successive powers of 2, less 1. The next series is found by doubling in turn each number of that series and adding the number that stands above the place where you write the result. The last row is obtained in the same way. This table will at once give solutions for any number of cheeses with three stools, for triangular numbers with four stools, and for pyramidal numbers with five stools. In these cases there is always only one method of solution—that is, of piling the cheeses.

In the case of three stools, the first and fourth rows tell us that 4 cheeses may be removed in 15 moves, 5 in 31, 7 in 127. The second and fifth rows show that, with four stools, 10 may be removed in 49, and 21 in 321 moves. Also, with five stools, we find from the third and sixth rows that 20 cheeses require 111 moves, and 35 cheeses 351 moves. But we also learn from the table the necessary method of piling. Thus, with four stools and 10 cheeses, the previous column shows that we must make piles of 6 and 3, which will take 17 and 7 moves respectively—that is, we first pile the six smallest cheeses in 17 moves on one stool; then we pile the next 3 cheeses on another stool in 7 moves; then remove the largest cheese in 1 move; then replace the 3 in 7 moves; and finally replace the 6 in 17: making in all the necessary 49 moves. Similarly we are told that with five stools 35 cheeses must form piles of 20, 10, and 4, which will respectively take 111, 49, and 15 moves.

If the number of cheeses in the case of four stools is not triangular, and in the case of five stools pyramidal, then there will be more than one way of making the piles, and subsidiary tables will be required. This is the case with the Reve's 8 cheeses. But I will leave the reader to work out for himself the extension of the problem.

*Si ignoras el significado de alguna palabra, utiliza el diccionario online.